FVANNUITY( ) 関数
一定の利率を使って計算した一連の預金額の将来価値を返します。将来価値は、毎月の預金額と複利利息の合計です。
構文
FVANNUITY(利率, 期間, 支払金額 <,種類>)
パラメーター
| 名前 | 型 | 説明 |
|---|---|---|
| 利率 | 数値 |
1 期あたりの利率。 |
| 期間 | 数値 |
支払期間の総数。 |
| 支払金額 | 数値 |
1 期間あたりの支払金額。 年金期間中、支払金額は毎回同じ金額でなければなりません。 |
|
種類 省略可能 |
数値 |
支払いのタイミング:
支払いのタイミングが省略された場合は、デフォルト値の 0 が使用されます。 |
メモ
利率、期間、支払金額を指定する際には、1 期あたりの利率を確実に指定するため、整合性のある期間を使用する必要があります。
例:
- 年利 5% の 2 年間の貸付金または投資に対して月払いする場合は、利率に 0.05/12、期間に 2 * 12 を指定します。
- 同じ貸付金または投資に対して年払いする場合は、利率に 0.05、期間に 2 を指定します。
出力
数値。結果は小数点以下 2 桁まで計算されます。
例
基本的な例
月次支払額
2 年間、毎月月初に支払う $1,000 の将来価値(月利 1% の複利)として、($)27243.20 が返されます。
FVANNUITY(0.01, 12, 1000, 1)
同じ年金の 1 年後の将来価値として、($)12809.33 が返されます。
FVANNUITY(0.01, 2*12, 1000, 1)
年次支払額
2 年間、毎年年末に支払う $12,000 の将来価値(年利 12% の複利)として、($)25440.00 が返されます。
FVANNUITY(0.12, 2, 12000, 0)
高度な例
年金の計算
年金の計算では、次の 4 つの変数が使用されます。
- 現在価値または将来価値 下の例では $21,243.39 と $ 26,973.46
- 1 期間あたりの支払金額 下の例では $1,000.00
- 1 期間あたりの利率 下の例では月あたり 1%
- 期間の数 下の例では 24 か月
これらの変数のうち 3 つの値がわかっている場合は、Analytics 関数を使って残りの変数の値を計算できます。
| 求めたい値: | 使用する Analytics 関数 |
|---|---|
| 現在価値 |
PVANNUITY( ) 21243.39 を返す: FVANNUITY(0.01, 12, 1000) |
| 将来価値 |
FVANNUITY( ) 26973.46 を返す: FVANNUITY(0.01, 24, 1000) |
| 1 期間あたりの支払金額 |
PMT( ) 1000 を返す: PMT(0.01, 24, 21243.39) |
| 1 期間あたりの利率 |
RATE( ) 0.00999999(1%)を返す: RATE(24, 1000, 21243.39) |
| 期間の数 |
NPER( ) 24.00 を返す: NPER(0.01, 1000, 21243.39) |
年金の式
期末年金(期末払い)の現在価値を計算する式:
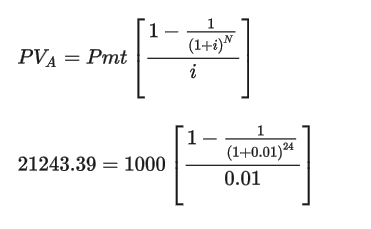
期末年金(期末払い)の将来価値を計算する式:
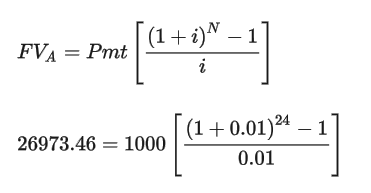
備考
関連する関数
PVANNUITY( ) 関数は FVANNUITY( ) 関数の逆関数です。